ADSA

Homework 10

Read sections 25, 25.1 and 25.2 from CLRS

Please read this with the goal of using the knowledge to do the homework below.

Watch lectures

1. Running time of all-pair shortest path algorithms - Floyd-Warshall and Dynamic programming
2. All-pair shortest path using dynamic programming
3. Floyd–Warshall algorithm

Question 1

The time complexity of the Dijkstra’s algorithm, when the priority queue is implemented using Fibonacci heap, is O(VlgV+E) and that of the Bellman-Ford algorithm is O(VE). These are both single-source shortest path algorithms. One straight-forward technique to obtain all-pair shortest paths is to run one of these two algorithms for every vertex in the graph. This makes the running times O(V²lgV+VE)) and O(V²E)) respectively. What will be the running times for (a) sparse graph, (b) dense graph, in terms of E?

Question 2

If a dense graph does not have negative weights, is it theoritically equivalent (in terms of speed) to run Dijkstra’s algorithm |V| times instead of the Floyd-Warshall algorithm? Why?

Question 3

Mary wants to solve the single-source shortest path problem on a dense graph with negative weights but she has the Floyd-Warshall all-pair shortest path algorithm implemented already. It is ok (in terms of speed) to use the implementation that she already has? Explain.

Question 4

Original question: For the directed graph below, trace the dynamic programming implementation for calculating all-pair shortest path to obtain the all-pair shortest paths. Calculate L⁽¹⁾, L⁽²⁾, L⁽³⁾, L⁽⁴⁾, and L⁽⁵⁾. For the missing weights assume the following weights: {(1,2): 1, (1,5): -1, and (3,2):1}. Verify your answers using the implementation in the appendix. (There is a negative weight cycle so your answers may not match.)

Corrected question (please ignore this if you already submitted): For the directed graph below, trace the dynamic programming implementation for calculating all-pair shortest path to obtain the all-pair shortest paths. Calculate L⁽¹⁾, L⁽²⁾, L⁽³⁾, L⁽⁴⁾, and L⁽⁵⁾. For the missing weights assume the following weights: {(1,2): 1, (1,5): -1, and (3,2):10}. Verify your answers using the implementation in the appendix.

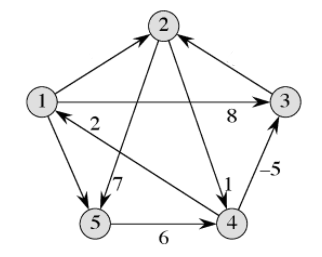
Question 5

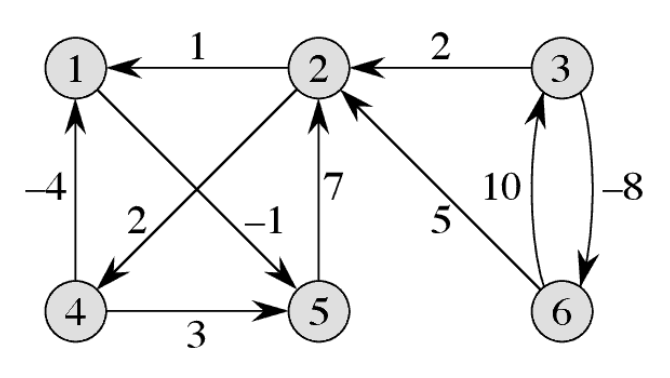
Run the Floyd-Warshall algorithm on the following weighted, directed graph and show the matrix D^(k) that results in each iteration of the outer loop. Here the input W is a n x n weight matrix where n is the number of vertices. d_ij^(k) is the weight of the shortest path from vertex i to vertex j for which all intermediate vertices are in the set {1, 2, …, k}. When k = 0, d_ij⁽⁰⁾ = w_ij.

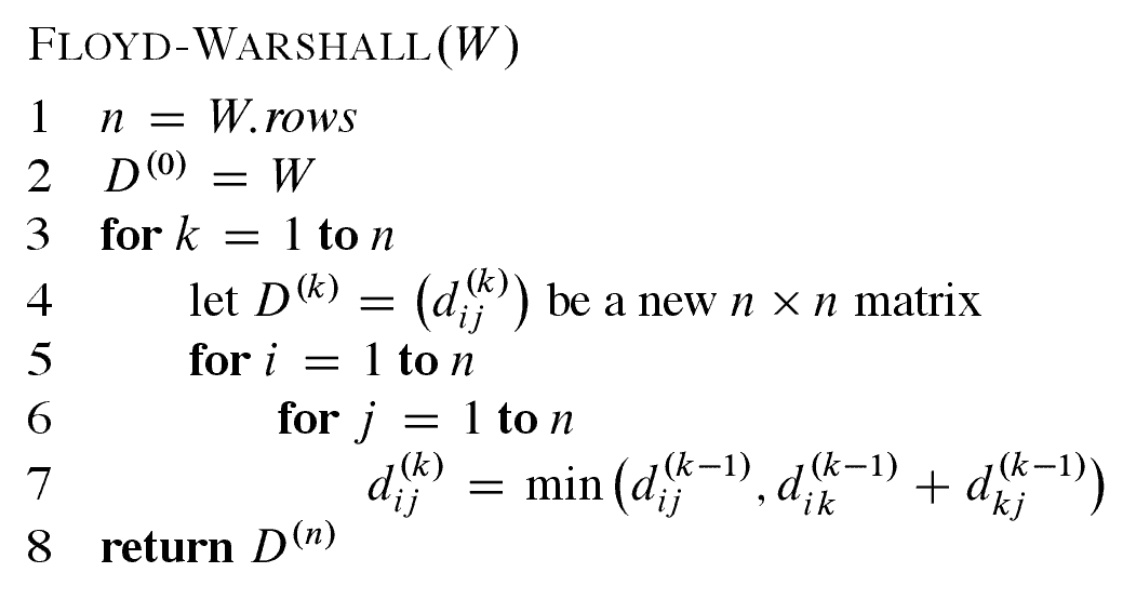
Question 6 (programming)

Find shortest paths between all ‘named’ places in the map of Silicon Valley below. As your answer, provide a table of all-pair shortest paths. You are welcome to use any ‘libraries’ or ‘publicly available code’.

Appendix

All-pair shortest path using dynamic programming (example, solution for a problem different from Q4)

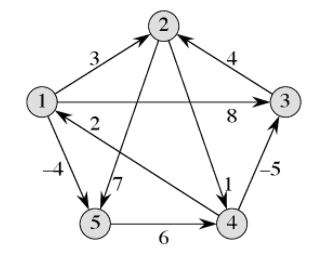
import numpy as np

W = np.array([[     0,      3,      8, np.inf,     -4],
              [np.inf,      0, np.inf,      1,      7],
              [np.inf,      4,      0, np.inf, np.inf],
              [     2, np.inf,     -5,      0, np.inf],
              [np.inf, np.inf, np.inf,      6,      0]])

def EXTEND_SHORTEST_PATHS(L, W):
    n = len(L[0, :])
    LL = np.full_like(L, np.inf)
    for i in range(n):
        for j in range(n):
            for k in range(n):
                LL[i, j] = min(LL[i, j], L[i, k] + W[k, j])
    return LL

def FASTER_ALL_PAIRS_SHORTEST_PATHS(W):
    n = len(W[0, :])
    LM = np.copy(W)
    m = 1
    while m < n:
        LM = EXTEND_SHORTEST_PATHS(LM, LM)
        m = 2 * m
    return LM

print('Graph:')
print(W)
print('All pair shortest path distances:')
print(FASTER_ALL_PAIRS_SHORTEST_PATHS(W))

Output:

Graph:
[[ 0.  3.  8. inf -4.]
 [inf  0. inf  1.  7.]
 [inf  4.  0. inf inf]
 [ 2. inf -5.  0. inf]
 [inf inf inf  6.  0.]]
All pair shortest path distances:
[[ 0.  1. -3.  2. -4.]
 [ 3.  0. -4.  1. -1.]
 [ 7.  4.  0.  5.  3.]
 [ 2. -1. -5.  0. -2.]
 [ 8.  5.  1.  6.  0.]]