ADSA

Homework 9

Read sections 24, 24.1, 24.2, and 24.3 from CLRS

Please read this with the goal of using the knowledge to do the homework below.

Understand the single-source shortest path problem

Watch lectures

Question 1

Trace the Dijkstra’s algorithm to obtain shortest paths to all other nodes from the node s. Assume that the weights for the edge (y,x) is 3 and (t,z) is 4.

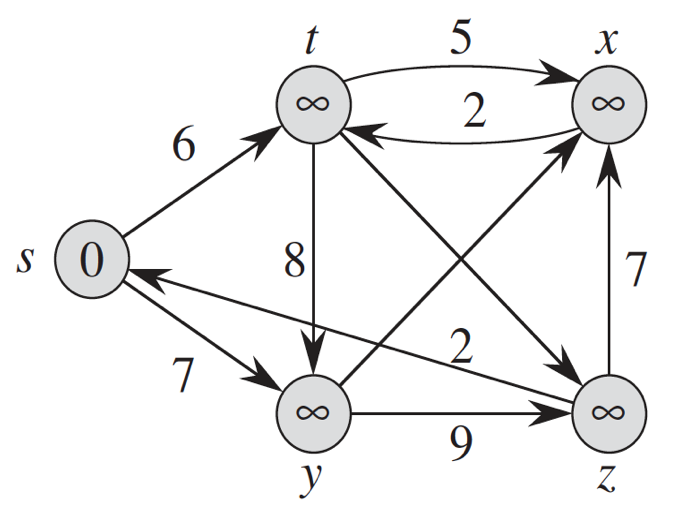
Question 2 (optional)

Question 3

A shortest path cannot contain a negative weight cycle. Nor can it contain a positive weight cycle. Because we can get a shorter path by removing such a cycle. Negative weight cycles in a directed graph can be an issue when computing shortest paths. Can we compute a shortest path from a to g in the graph below using the Dijkstra’s algorithm or Bellman-Ford algorithm? Explain.

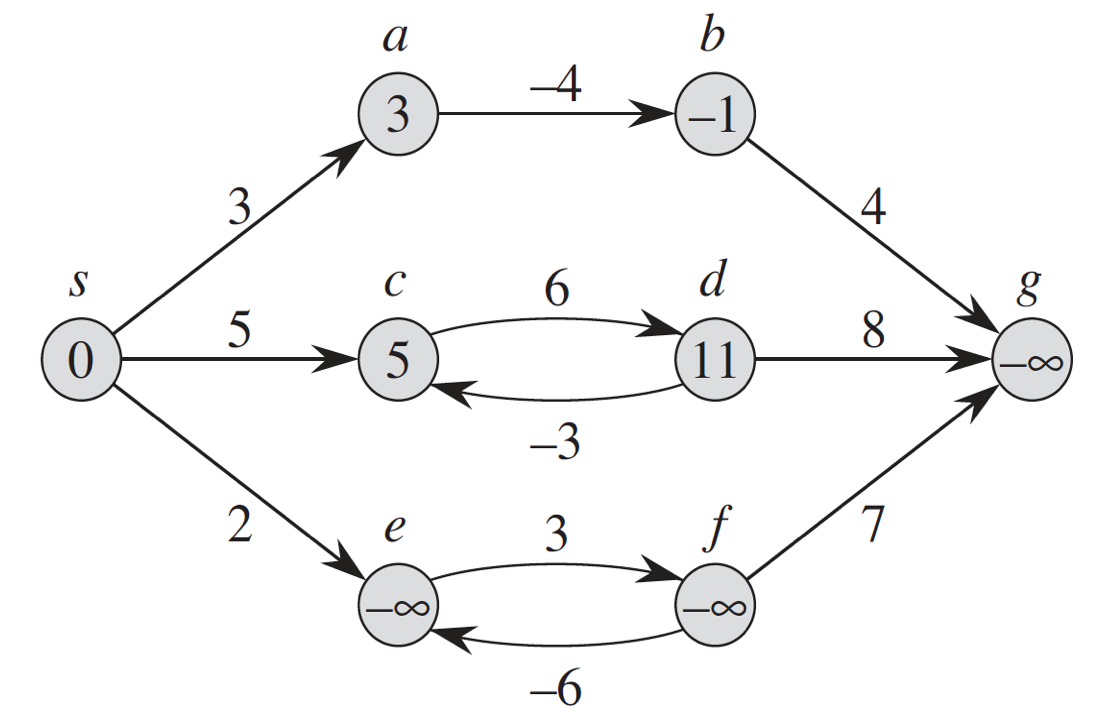
Question 4

In the Dijkstra’s algorithm (above), assume that the cost of each EXTRACT-MIN operation is O(lg V). If each RELAX operations takes O(V) time, what will be time complexity of the overall algorithm terms of Big-O?

Question 5

Shortest paths are always well defined in a directed acyclic graph (DAG). This is because even if there are negative weight edges, no negative-weight cycles can exist. Hence, we don’t need to run Dijkstra’s algorithm or Bellman-Ford algorithm. A faster algorithm DAG-SHORTEST-PATHS(G, w, s) (G is the graph (V,E), w is weight matrix, and s is starting node) with a running time of Θ(V+E) can be used to calculate the shortest paths in DAGs (see below).

An interesting application of this arises in determining ‘critical paths’, i.e. paths with lowest cost. For the directed acyclic graph below that shows the time needed to perform various activities to bake a cake, determine a critical path (i.e. the quickest we could bake the cake) using the algorithm DAG-SHORTEST-PATHS() below. In the graph, edges represent jobs to be performed, and edge weights represent the times required to perform particular jobs. If edge (u,v) enters vertex v and edge (v, x) leaves v, then job (u,v) must be performed before job (v,x). A path through this DAG represents a sequence of jobs that must be performed in a particular order. A critical path is a longest weighted path through the DAG that corresponds to the overall time needed to complete all the jobs. The weight of a critical path provides a lower bound on the total time to perform all the jobs.

Since we are actually interested in the ‘minimum’ time, the weights (time in minutes) must be negated before running the algorithm below. This will translate the problem of finding longest path to finding shortest path in a DAG. Alternately, the standard RELAX() and INITIALIZE-SINGLE-SOURCE() will need to be updated as shown below.

In addition to determining a critical path, show your topological ordering. Clearly show how the RELAX() operation changes the value of ‘shortest path estimate’ and ‘predecessor attribute’ of the Node 7. Nodes should be processed in the order of their numbers.

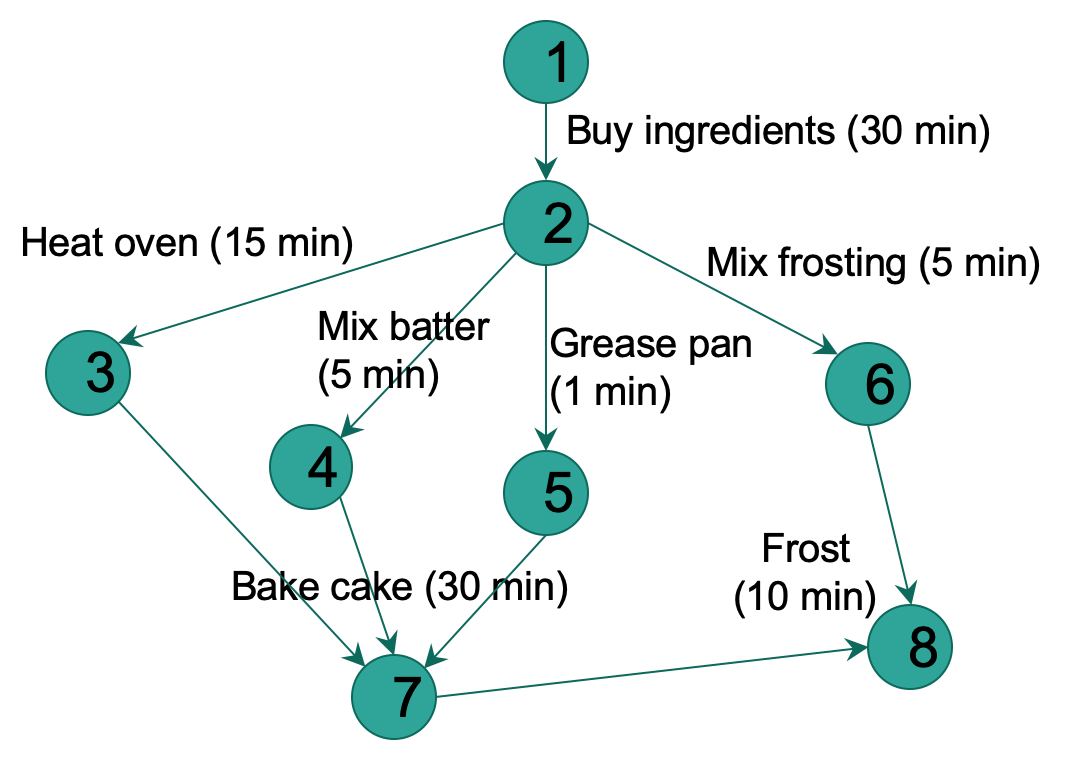
Question 6

For the following graph, in how many executions of the ‘outer for loop’ (line #2) will the Bellman-Ford algorithm find the shortest-paths, if you consider edges by:

Non-decreasing weights (starting with the smallest weight)?
Non-increasing weights (starting with the largest weight)?
In the following order: (t,x), (t,y), (t,z), (x,t), (y,x), (y,z), (z,x), (z,s), (s,t), (s,y)?

Can we conclude that selecting edges by non-increasing or non-decreasing weights will make the algorithm converge faster?

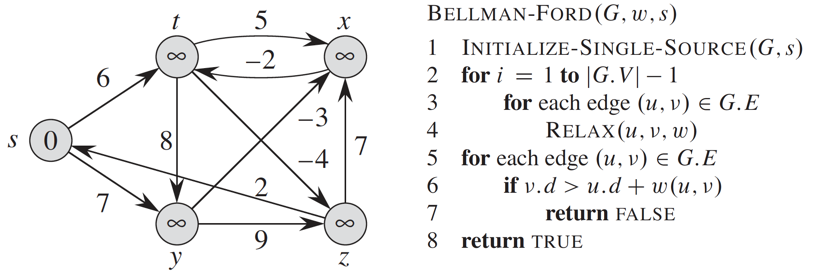
Question 7 (programming)

Find shortest paths between Mountain View and all other places in the map of Silicon Valley below. As your answer, provide the list of all the places and their corresponding shortest distance sorted by the shortest distance. You are welcome to use any ‘libraries’ or ‘publicly available code’. You can choose to either collapse the ‘unlabelled’ nodes or remove the nodes and the associated paths. When converting the graph’s undirected to directed edges, you can either assume random directions or create two directed edges (with same weight) for one undirected edge.