ADSA

Homework 8

Read sections 23.1 and 23.5 from CLRS

Please read this with the goal of using the knowledge to do the homework below.

Understand the muddy city problem

The muddy city problem

Watch lectures

What is a minimum spanning tree?

The Kruskal’s algorithm

Intuition of Kruskal’s algorithm
Kruskal’s GIF
The Find() and Union() methods in disjoint set (only the first two minutes, i.e. skip the implementation)
Tracing the Kruskal’s algorithm (only up to 4:43, i.e. skip the implementation)

The Prim’s algorithm

Intuition of Prim’s algorithm
Prim’s GIF
Tracing the Prim’s algorithm (first five minutes only, i.e. skip the implementation)

How do the Kruskal’s and Prim’s algorithms work?

The cut property

Question 1 (partial programming)

Assign the houses in the muddy city map the names of US states, and draw it as a weighted graph. Assume that paving the bridge costs three times more than one stone. Obtain a solution using your own intuition/hit-and-trial, without using any computing techniques. Verify your solution using the NetworkX library (see example code block below).

import networkx as nx
G = nx.Graph()
G.add_edge('a', 'b', weight = 4)
G.add_edge('b', 'c', weight = 8)
MST = nx.minimum_spanning_tree(G)
nx.draw(G, alpha = 0.8, with_labels = True)

Question 2

Say that we have a larger muddy city with N houses. To interconnect all the houses, we can use an arrangement of N-1 roads, each connecting two houses. Assuming that the cost of connecting any two houses is fixed (same), how many arrangements are possible (in terms of N)? Hint 1: Consider the worst case scenario, i.e. the graph could be a complete graph. Hint 2: The answer is not N² or N! or (N-1)! or N(N-1)/2. Hint 3: Try with N = 3, 4, and 5.

Question 3 (partial programming)

Showing all the intermediate steps, obtain a MST using Kruskal’s algorithm for the graph below. Assume the following weights between the nodes that have missing weights: A-B:11, B-C:9, A-F:2, F-G:13, and G-H:4. An example solution, for a different problem, is here. After obtaining the answer, verify your solution using the NetworkX library.

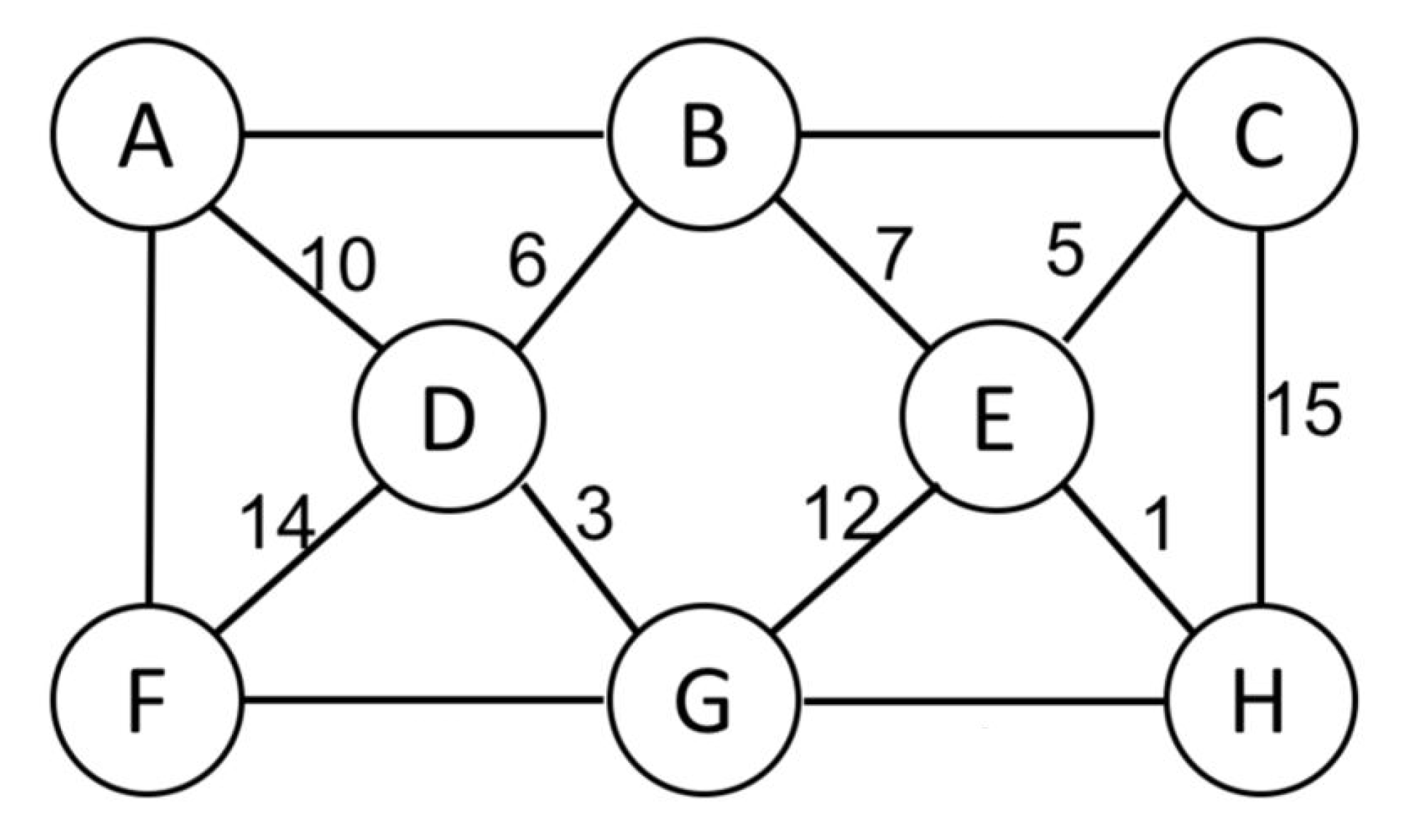
Question 4 (partial programming)

Showing all the intermediate steps, obtain a MST using Prim’s algorithm for the graph above (same graph but slightly different weights). Assume the following weights between the nodes that have missing weights: A-B:11, B-C:9, A-F:12, F-G:13, and G-H:4. Note that the weights are slightly different. An example solution, for a different problem, is here. After obtaining the answer, verify your solution using the NetworkX library.

Question 5

Consider the Prim’s algorithm below. Here, G represents the graph, w is the 2D weight matrix, and r is the starting vertex. Q is a minimum priority queue. v.key is the distance from the current minimum spanning tree to v and v.𝝅 is for storing the parent of v.

We are interested to calculate the time complexity (running time) of the algorithm in terms of big-O by analyzing the time taken by the various segments of the algorithm.

Segment 1. These initializations take O(V) time.
Segment 2. The total time for all calls to Extract-Min(Q) operations is O(V * time for Extract-Min(Q)). The time complexity of Extract-Min(Q) is O(lgV). On the other hand, if priority queue is implemented using Fibonacci heap, the time complexity is O(1).
Segment 3. We scan the adjacency list of each vertex once which takes O(E) time. Let’s assume that the time needed for v.𝝅 = u and v.key = w(u,v) is t so that total time is O(t * E). Every time the v.key and v.𝝅 are updated, the priority queue (heap) has to be updated.

Calculate the time complexity of the MST-PRIM() algorithm in terms of the three segments.

Question 6

A dense graph is a graph in which the number of edges is close to the maximal number of edges, and a sparse graph is a graph in which the number of edges is close to the minimal number of edges. The running time of Kruskal’s algorithm is O(E lg V) and the running time of Prim’s algorithm (when we use Fibonacci heap for priority queue) is O(E + V lgV). Is the following statement correct, “Prim’s algorithm is a better (faster) choice when you want to find MST for a dense graph”? Explain.

Question 7

One may argue that for a problem such as the muddy city problem, if a few ‘genius’ people spend an hour or two on the problem it can be easily solved, and that there is no need to find a ‘computer programmer’ to translate the problem into a programming problem and run these MST algorithms to find a solution. In addition, the person may further argue that having an algorithm is enough, there is no need to analyze the big-O and precisely choose an algorithm. Do you agree? Provide your reasons. Hint: Read the applications of MST algorithms.

Question 8

How does the cut property apply to (a) Kruskal’s algorithm, and (b) Prim’s algorithm? Hint: Rewatch the the lectures that explain how the two algorithms work and analyze the connection between the cut property and the two algorithms.